范数
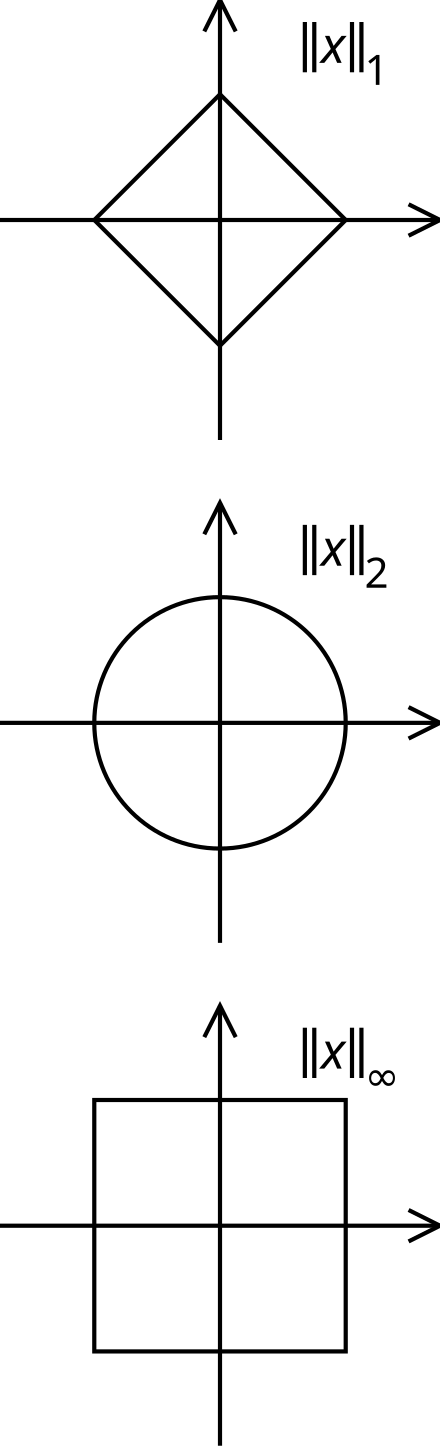
定义 Link to heading
范数,是具有“长度”概念的函数。
绝对值范数 Link to heading
绝对值 范数为
$$ \left \| x \right \| = \sum_{i}^{n} \left | x_{i} \right | $$是在由实数或虚数构成的一维向量空间中的范数。
绝对值范数是 曼哈顿范数 的特殊形式。
绝对值 范数为
是在由实数或虚数构成的一维向量空间中的范数。
欧几里德范数 Link to heading
在 n 维 欧几里德空间 ${\displaystyle \mathbb {R} ^{n}}$上,向量${\displaystyle {\boldsymbol {x}}=(x_{1},x_{2},\ldots ,x_{n})^{\mathrm {T} }}$的最符合直觉的长度由以下公式给出
$$ {\displaystyle \\|{\boldsymbol {x}}\\|_{2}:={\sqrt {x_{1}^{2}+\cdots +x_{n}^{2}}}.}$$欧几里得距离 Link to heading
在欧几里得空间中,点$ x =( x_1 ,...,x_n) $和 $ y =( y_1,...,y_n)$之间的欧氏距离为
$$ \displaystyle d(x,y)={\sqrt {(x_{1}-y_{1})^{2}+(x_{2}-y_{2})^{2}+\cdots +(x_{n}-y_{n})^{2}}} $$