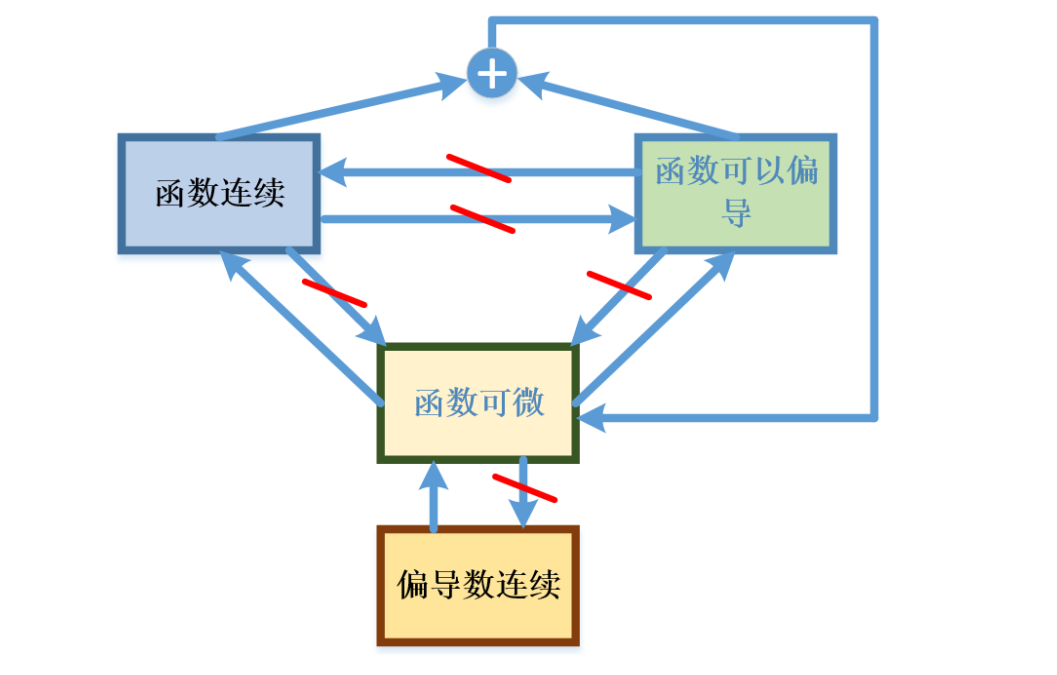
函数连续、可微、可导之间的关系
偏导数与可偏导的区别 Link to heading
$
\frac{\partial y}{\partial x}
$
表示对 $x$ 的偏导数,而可以偏导是指一个函数是否具有偏导数。并不是所有的函数都具有偏导数。
例如,如果一个函数在某一点上不连续或者有尖锐的转折,那么在该点上它可能没有偏导数。

$
\frac{\partial y}{\partial x}
$
表示对 $x$ 的偏导数,而可以偏导是指一个函数是否具有偏导数。并不是所有的函数都具有偏导数。
例如,如果一个函数在某一点上不连续或者有尖锐的转折,那么在该点上它可能没有偏导数。