CNN卷积神经网络
数学原理 Link to heading
卷积公式 Link to heading
设随机变量$(X,Y)$的联合密度函数为 $f(X,Y)$ 且$X$的边缘密度函数为$f_X(x)$的边缘密度函数为$f_Y(y)$. 则随机变量$(X,Y)$的函数$Z =X+Y $的密度函数为
$$
f_Z(z) = \int_{-\infty}^{\infty} f(z-y,y)dy
$$
特别地,当$X$和$Y$相互独立时,$f_Z(z)$为
$$
f_Z(z) = \int_{-\infty}^{\infty} f_X(z-y)f_Y(y)dy
$$
Dropout Link to heading
在神经网络的训练过程中,对于一次迭代中的某一层神经网络,先随机选择中的一些神经元并将其临时隐藏(丢弃),然后再进行本次训练和优化。在下一次迭代中,继续随机隐藏一些神经元,如此直至训练结束。由于是随机丢弃,故而每一个mini-batch都在训练不同的网络。
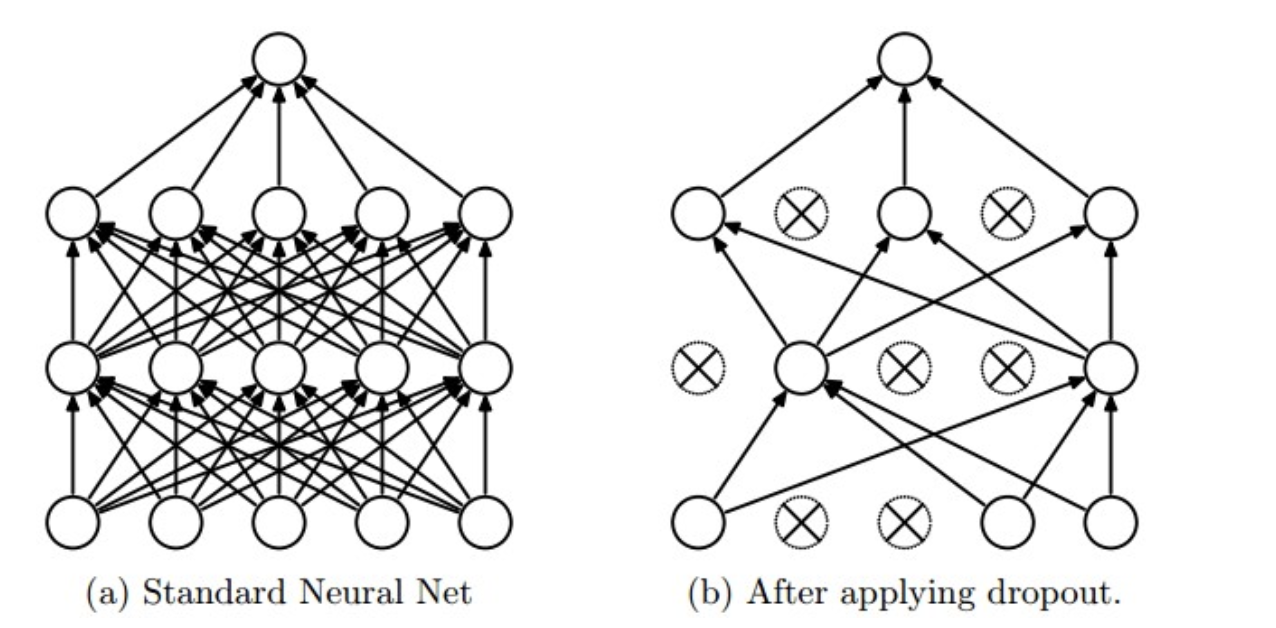
与之类似地,卷积神经网络如下图应用前(下方)后(上方)如下图:

图像处理 Link to heading
输入通道 Link to heading
对于图像数据,输入通道通常表示图像的颜色通道。例如:
灰度图像:1 个通道(黑白)。
RGB 彩色图像:3 个通道(红、绿、蓝)。
在卷积操作中,输入通道的数量决定了卷积核的深度。每个卷积核的深度必须与输入通道数一致。
输出通道 Link to heading
每个输出通道是通过一个独立的卷积核计算得到的。
输出通道的数量决定了卷积层提取的特征图的数量。例如:
如果输出通道数为 32,则表示有 32 个不同的卷积核,每个卷积核提取一种特征。
卷积核 Link to heading
卷积核(或滤波器)是一个小矩阵,用于在输入数据上滑动并计算局部区域的加权和。
每个卷积核的深度与输入通道数相同,而卷积核的数量与输出通道数相同。
例如: 输入通道数为 3(RGB 图像),输出通道数为 32。则需要 32 个卷积核,每个卷积核的深度为 3。
池化层 Link to heading
池化层 是一个利用 池化函数 (pooling function) 对网络输出进行进一步调整的网络层。池化函数使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出。常用的池化函数包括最大池化 (max pooling) 函数 (即给出邻域内的最大值) 和平均池化 (average pooling) 函数 (即给出邻域内的平均值) 等。但无论选择何种池化函数,当对输入做出少量平移时,池化对输入的表示都近似 不变 (invariant)。局部平移不变性 是一个很重要的性质,尤其是当我们关心某个特征是否出现而不关心它出现的位置时。
池化层同卷积层类似
区别 Link to heading
| 特性 | 卷积层 | 池化层 |
|---|---|---|
| 功能 | 提取局部特征,生成特征图。 | 降维和压缩特征图,保留主要特征。 |
| 操作 | 卷积操作(加权求和)。 | 池化操作(如最大值、平均值)。 |
| 参数 | 包含可学习的参数。 | 不包含可学习的参数。 |
| 输出通道数 | 由卷积核的数量决定。 | 与输入通道数相同。 |
| 空间尺寸变化 | 可能改变特征图的空间尺寸。 | 通常减小特征图的空间尺寸。 |
卷积层输出 Link to heading
卷积层的参数:
in_channels:输入通道数,这里是3。out_channels:输出通道数,这里是128。kernel_size:卷积核大小,这里是3x3。padding:填充大小,这里是1。stride:步幅,默认是1。
$$
\[
\text{output\_width} = \left\lfloor \frac{\text{width} + 2 \times \text{padding} - \text{kernel\_size}}{\text{stride}} \right\rfloor + 1
\]
$$
池化层的参数:
kernel_size:池化窗口大小,这里是2x2。stride:步幅,这里是2。