BP神经网络
感知机 Link to heading
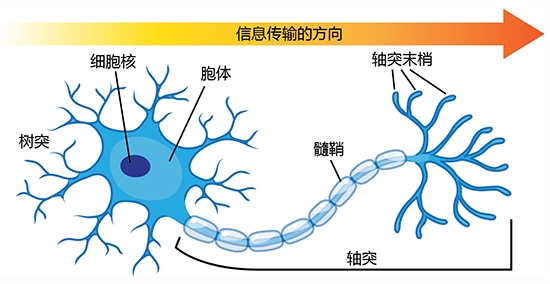
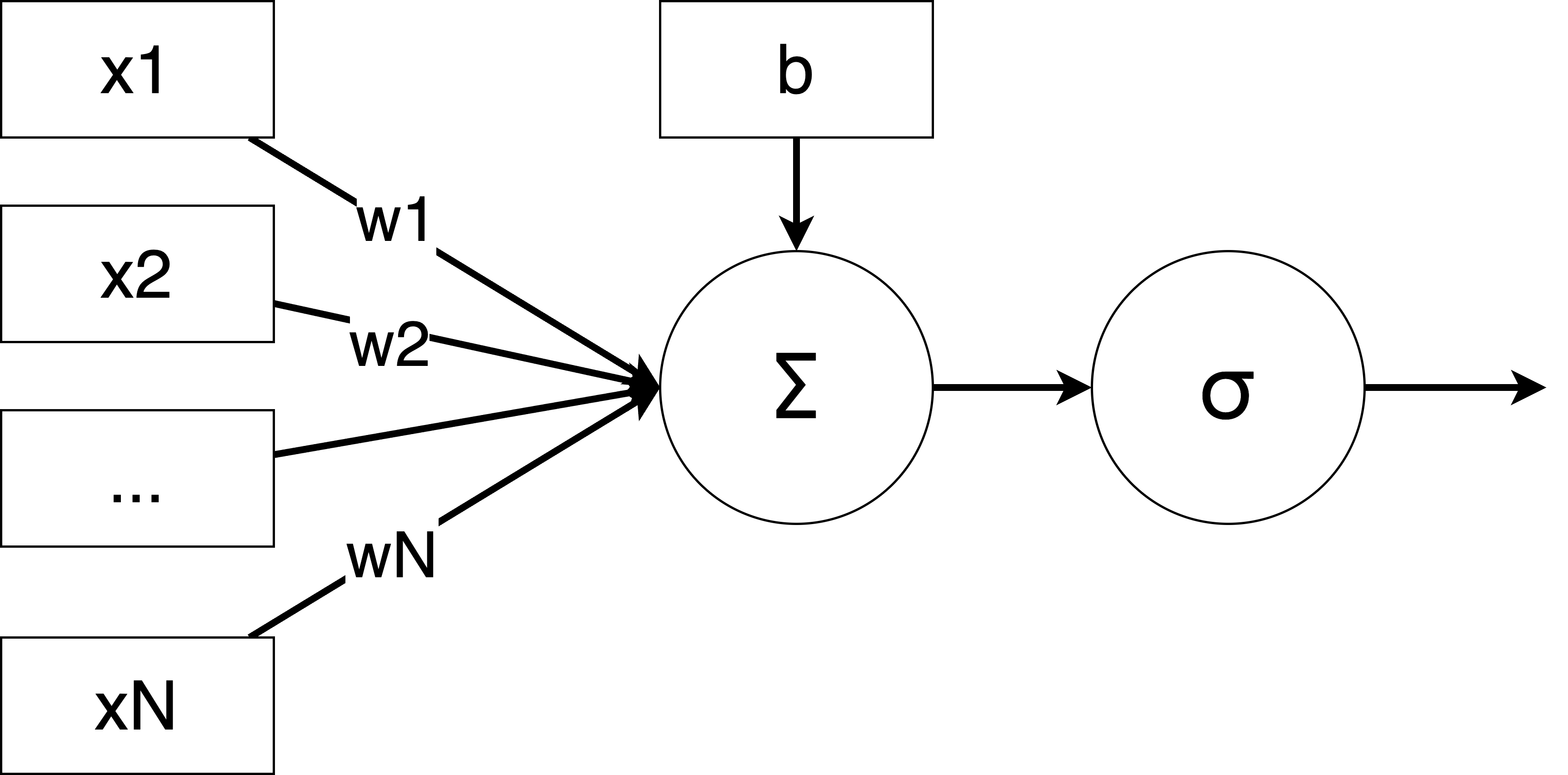
感知机就是模拟神经元从接收输入信号传递输出信号的过程,如果加权和超过了一个阈值,神经元激活,输出信号;否则神经元不激活,不输出信号。感知机接收输入信号,通过加权和激活函数输出信号。
损失函数 Link to heading
损失函数用来衡量模型预测结果与真实值之间的差距。值越小,说明模型的预测越准确;值越大,说明预测越不准确。
梯度下降 Link to heading
梯度下降是一种优化算法,用来最小化损失函数。
梯度下降通过计算损失函数的梯度,沿着梯度的反方向(即损失下降最快的方向)更新参数,逐步逼近损失函数的最小值。
梯度消失 Link to heading
梯度消失是指在反向传播过程中,梯度逐渐变小,最终趋近于零,导致网络参数几乎无法更新。
mini batch 梯度下降 Link to heading
每次使用一小部分数据计算梯度并更新参数
随机梯度下降 Link to heading
每次使用一个数据计算梯度并更新参数
批量梯度下降 Link to heading
每次使用所有数据计算梯度并更新参数
原因 Link to heading
激活函数:使用如Sigmoid或Tanh等激活函数时,其导数在输入值较大或较小时会趋近于零。多层叠加后,梯度会不断缩小。
深层网络:网络层数越多,梯度在传播过程中缩小的可能性越大。
梯度爆炸 Link to heading
梯度爆炸是指在反向传播过程中,梯度逐渐变大,最终导致参数更新过大,模型无法收敛。
原因 Link to heading
权重初始化不当:权重初始值过大,导致梯度在传播过程中不断放大。
深层网络:层数越多,梯度放大的可能性越大。
激活函数 Link to heading
激活函数会决定一个神经元的输出是否传递给下一层。如果输出值很大,神经元就“激活”;如果输出值很小,神经元就“抑制”。
激活函数(Activation Function)是神经网络中的一个重要组成部分。它的作用是为神经网络引入非线性,使得神经网络能够学习复杂的模式和关系。如果没有激活函数,神经网络就只是一个线性模型,无论有多少层,都只能解决简单的线性问题。
通俗解释 Link to heading
想象你在玩一个游戏,任务是判断一张图片是猫还是狗。你的大脑会通过一系列的“判断”来完成这个任务:
- 图片中有耳朵吗?
- 耳朵是尖的还是圆的?
- 图片中有尾巴吗?
- 尾巴是长的还是短的?
这些“判断”就是神经网络的“神经元”在做的事情。而激活函数的作用就是决定这些“判断”是否足够强,是否需要传递给下一层。
- 如果没有激活函数:神经网络的每一层只能做简单的线性计算,就像你只能回答“是”或“不是”,无法处理复杂的判断。
- 有了激活函数:神经网络可以学习更复杂的规则,比如“如果耳朵是尖的,而且尾巴是长的,那么可能是猫”。
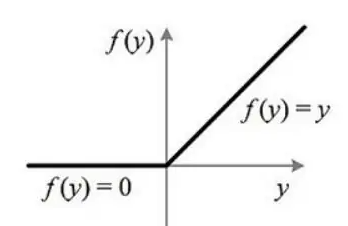
ReLU激活函数 Link to heading
$$
f(x) = max(0, x)
$$
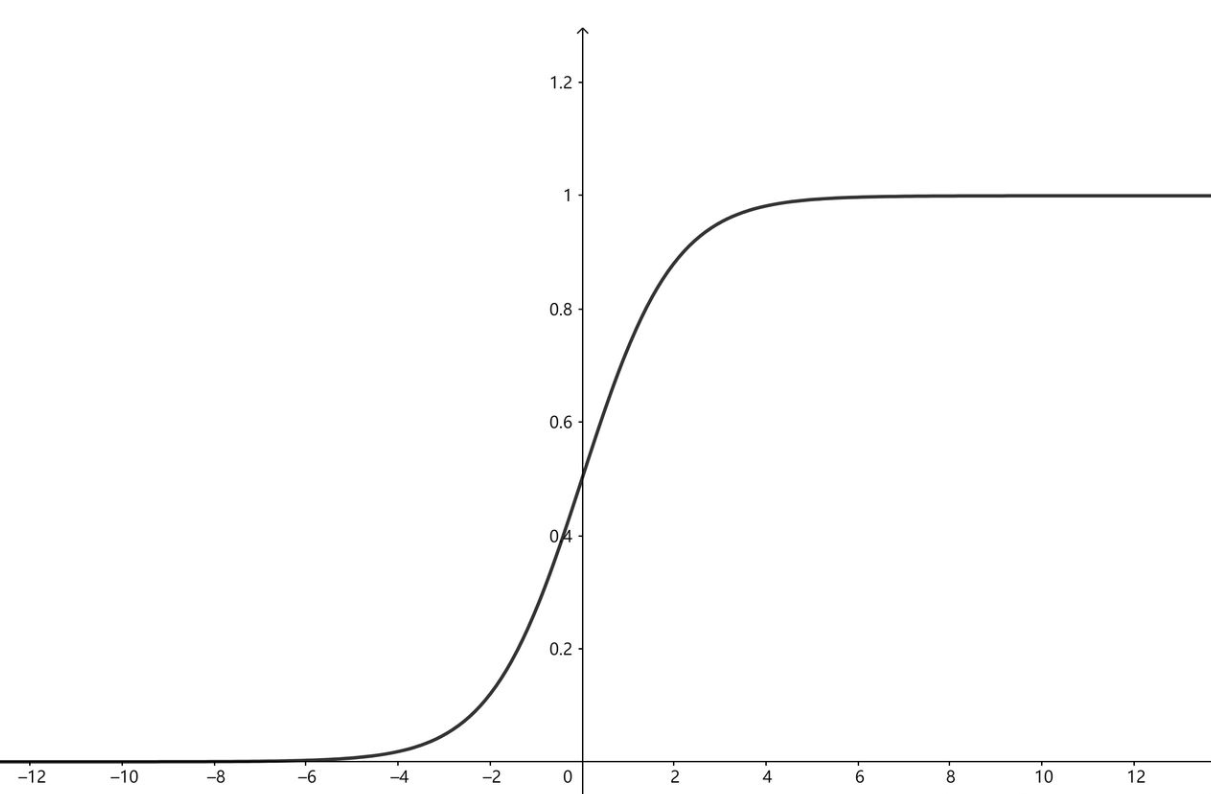
Sigmoid激活函数 Link to heading
$$
f(x) = \frac{1}{1 + e^{-x}}
$$
前向传播 Link to heading
前向传播就是根据输入数据和权重,通过激活函数,计算网络的输出。
指数移动平均 Link to heading
指数移动平均是一种常用的平滑技术,用于对时间序列或序列数据进行加权平均。它的核心思想是对当前值和历史值赋予不同的权重,使得最近的数据对平均值的影响更大,而历史数据的影响逐渐衰减。
EMA 在深度学习中常用于以下场景:
- Batch Normalization:用于更新全局均值和方差。
- 模型权重平滑:在训练过程中对模型权重进行平滑,提高模型的鲁棒性。
- 时间序列预测:对时间序列数据进行平滑处理。
EMA 的计算公式如下:
$$ \text{EMA}_t = \alpha \cdot x_t + (1 - \alpha) \cdot \text{EMA}_{t-1} $$其中:
- $\text{EMA}_t$:当前时刻的指数移动平均值。
- $x_t$:当前时刻的观测值。
- $\text{EMA}_{t-1}$:上一时刻的指数移动平均值。
- $\alpha$:平滑系数(也称为衰减因子),取值范围为$0 < \alpha \leq 1$。
反向传播 Link to heading
反向传播就是根据前向传播后的结果与真实值之间的误差,通过链式法则,更新权重。
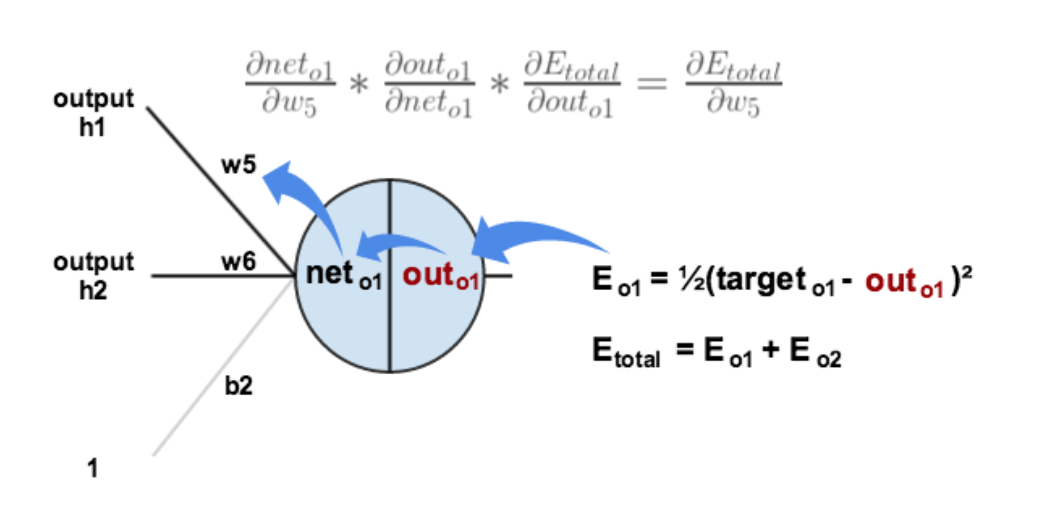
其中net是神经元的输入,out是神经元的输出,net是加权后的结果,out是激活函数后的结果。
正则化 Link to heading
正则化就像“适度复习”,帮助模型在训练时不过度依赖训练数据,从而提升泛化能力。
L1正则化 Link to heading
L1正则化在损失函数中添加模型参数的绝对值之和作为惩罚项。
$$ \text{损失函数} = \text{原始损失函数} + \lambda \sum_{i=1}^{n} |w_i| $$- $w_i$ 是模型的参数。
- $\lambda$ 是正则化强度。
特点 Link to heading
- 稀疏性:L1正则化倾向于将一些参数压缩到0,适合特征选择。
- 鲁棒性:对异常值不敏感。
L2正则化 Link to heading
L2正则化在损失函数中添加模型参数的平方和作为惩罚项。
$$ \text{损失函数} = \text{原始损失函数} + \lambda \sum_{i=1}^{n} w_i^2 $$- $w_i$ 是模型的参数。
- $\lambda$ 是正则化强度。
特点 Link to heading
- 平滑性:L2正则化让参数接近0但不为0,适合处理共线性问题。
- 稳定性:对异常值敏感。
Batch Normalization Link to heading
Batch Normalization主要目的是通过标准化每一层的输入,加速神经网络的训练过程,并提高模型的稳定性和性能。
在深度神经网络中,每一层的输入分布会随着前一层参数的变化而发生变化,这种现象称为 Internal Covariate Shift(内部协变量偏移)。这种分布的变化会导致训练过程变得不稳定,尤其是深层网络。
Batch Normalization 通过对每一层的输入进行标准化,强制使其分布保持稳定,从而缓解 Internal Covariate Shift 问题。
BN的原理 Link to heading
假设我们有一个 mini-batch 数据 $\mathcal{B} = \{x_1, x_2, \dots, x_m\}$,Batch Normalization 的操作步骤如下:
计算 mini-batch 的均值和方差 Link to heading
对于每个特征维度(通常是每个神经元的输出),计算 mini-batch 的均值 $\mu_\mathcal{B}$ 和方差 $\sigma_\mathcal{B}^2$:
$$ \mu_\mathcal{B} = \frac{1}{m} \sum_{i=1}^m x_i $$$$ \sigma_\mathcal{B}^2 = \frac{1}{m} \sum_{i=1}^m (x_i - \mu_\mathcal{B})^2 $$标准化 Link to heading
使用均值和方差对 mini-batch 进行标准化:
$$ \hat{x}_i = \frac{x_i - \mu_\mathcal{B}}{\sqrt{\sigma_\mathcal{B}^2 + \epsilon}} $$其中 $\epsilon$ 是一个很小的常数(例如 $10^{-5}$),用于防止除零错误。
缩放和平移 Link to heading
为了保留网络的表达能力,引入可学习的参数 $\gamma$(缩放因子)和 $\beta$(平移因子):
$$ y_i = \gamma \hat{x}_i + \beta $$其中 $\gamma$ 和 $\beta$ 是通过训练学习的参数。
BN的作用 Link to heading
加速训练 Link to heading
- 通过标准化输入分布,减少了 Internal Covariate Shift,使得每一层的输入更加稳定。
- 允许使用更大的学习率,从而加速收敛。
缓解梯度消失和梯度爆炸 Link to heading
- 标准化后的输入分布更加稳定,梯度在反向传播过程中更容易传播。
正则化效果 Link to heading
- Batch Normalization 引入了噪声(因为 mini-batch 的均值和方差是估计值),起到了一定的正则化作用,可以减少过拟合。
减少对参数初始化的依赖 Link to heading
- 由于输入分布被标准化,网络对参数初始化的敏感性降低。
注意事项 Link to heading
- 训练阶段:使用 mini-batch 的均值和方差进行标准化。
- 测试阶段:使用训练过程中计算的全局均值和方差(通常通过指数移动平均得到)。
附录 Link to heading
一文弄懂神经网络中的反向传播法——BackPropagation